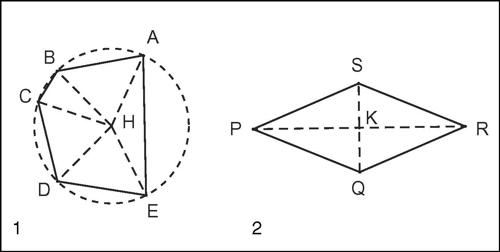
centro

Enciclopedia della Matematica (2013)

centro


centro in geometria e nell’uso comune, il centro di una figura è un particolare punto che viene definito in maniera diversa a seconda dei casi. Nella circonferenza e nella superficie sferica, il centro è il punto equidistante da tutti i punti della circonferenza o della superficie sferica stessa: ne rappresenta quindi il centro di simmetria. In particolare, in una circonferenza descritta in un sistema di riferimento cartesiano dall’equazione

formula

il centro ha coordinate (−a, −b). Il centro di un poligono inscrivibile in una circonferenza è il punto equidistante da tutti i vertici del poligono e quindi centro della circonferenza circoscritta al poligono stesso. In base a tale definizione tutti i triangoli hanno un centro (circocentro), mentre non tutti i poligoni con più di tre lati lo hanno. Per alcuni poligoni il centro è invece definito come centro di simmetria della figura, punto tale che ogni retta passante per esso contiene due punti della figura, da parti opposte rispetto a esso e a uguale distanza; è il caso del parallelogramma (e quindi del rombo) il cui centro è il punto di incontro delle diagonali. Le due definizioni a volte coincidono, come avviene per esempio per i poligoni regolari con un numero pari di lati e per i rettangoli, a volte non coincidono.

Nello spazio si hanno situazioni del tutto analoghe. Il centro di una sfera è il punto equidistante da tutti i punti della sua superficie. Per quanto riguarda i poliedri può essere estesa a essi la duplice definizione introdotta per i poligoni. Il centro di un poliedro è pertanto il punto, se esiste, equidistante dai suoi vertici, oppure il punto rispetto al quale il poliedro è simmetrico. Anche in tre dimensioni le due definizioni possono risultare equivalenti. Inteso come centro di simmetria il termine è associato anche a curve del piano o a superfici dello spazio, quali, per esempio, ellissi, iperboli, ellissoidi, iperboloidi. Il termine appare in diversi contesti geometrici, con significati specifici: per esempio, centro di → curvatura, centro di → proiezione, centro di → rotazione, centro di → omotetia, o ancora centro di simmetria in una → simmetria centrale).

Il termine è anche utilizzato in algebra in riferimento a particolari contesti (centro di un → gruppo, centro di un → anello).

CENTRO

Vedi anche
circonferenza In geometria, curva piana, luogo dei punti equidistanti da un punto fisso O, detto centro della c.; la superficie piana da essa racchiusa è il cerchio. La distanza costante dal centro a un punto qualsiasi della c. si chiama raggio; il doppio di essa, diametro. Molte nozioni e proprietà della c. sono ... punto Matematica Insieme alla retta e al piano, uno degli enti fondamentali della geometria, la cui nozione intuitiva corrisponde all’idea di una posizione sulla retta, nel piano o nello spazio (si tratta cioè di una figura non scomponibile in parti e priva di dimensioni); nella geometria euclidea, la nozione, ... curvatura Lo stato generico di un ente geometrico o fisico di scostarsi da un andamento rettilineo o piano. C. di una curva piana 1Elemento definito punto per punto della curva, che misura la rapidità con la quale la curva si discosta dalla tangente, la rapidità cioè con la quale essa si discosta dall’andamento ... ellisse In geometria, curva piana chiusa che si ottiene segando un cono circolare (retto od obliquo) con un piano non parallelo ad alcuna generatrice. Un caso particolare di e. è da considerarsi la circonferenza. L’e. è una curva piana del 2° ordine, cioè una conica. In coordinate cartesiane x, y, essa è rappresentata ...
Tag
Altri risultati per centro
  • centro
    Dizionario delle Scienze Fisiche (1996)
    cèntro [Der. del lat. centrum, dal gr. kéntron "punta di compasso"] [ALG] Per estensione del signif. proprio relativo a una circonferenza, punto che individua una simmetria di una figura geometrica o che gode di particolari proprietà, spesso ancora collegate con una qualche simmetria. ◆ [ASF] C. attivo: ...
  • CENTRO
    Enciclopedia Italiana (1931)
    In matematica questa parola assume diversi significati. Nell'uso più comune significa "centro di simmetria" di una figura piana o spaziale. In questo senso hanno un centro, nel piano, i poligoni regolari, il cerchio e, più in generale, le curve algebriche del 2° ordine o coniche (v.), eccettuate le ...
Vocabolario
centrare
centrare v. tr. [der. di centro] (io cèntro, ecc.). – 1. Fissare nel centro: c. la punta del compasso. 2. Far corrispondere il centro di due circoli; più in generale, far corrispondere il centro di una figura (o di un oggetto) con quello...
cèntro
centro cèntro s. m. [dal lat. centrum, e questo dal gr. κέντρον «aculeo; punta di compasso; centro»]. – 1. In geometria, c. di una circonferenza, il punto equidistante da ogni punto della circonferenza; analogam., c. di una sfera. Più in...