discontinuita

discontinuita

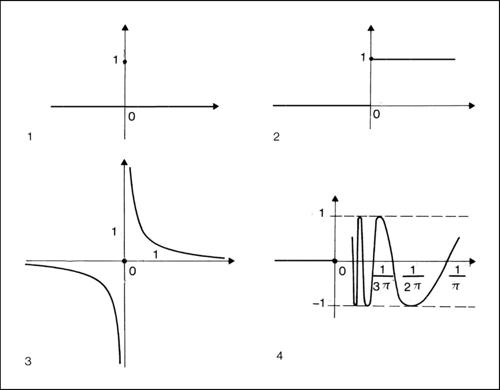
discontinuità termine utilizzato in connessione con la nozione di → continuità. Si dice punto di discontinuità di una funzione reale di variabile reale y = ƒ(x) un punto x₀ del suo dominio in cui ƒ è non continua. Una funzione di questo tipo può avere tre tipi di discontinuità in un punto x₀: discontinuità di prima specie, o di salto, se i due limiti destro e sinistro di y per x tendente a x₀ esistono, sono finiti ma diversi tra loro (la discontinuità non è eliminabile); discontinuità di seconda specie se almeno uno dei due limiti è infinito o non esiste (anche in questo caso la discontinuità non è eliminabile); discontinuità di terza specie o eliminabile se i due limiti sono uguali e finiti, ma diversi dal valore della funzione (con opportuni accorgimenti la discontinuità è eliminabile). Frequentemente, anche se in modo improprio, si danno i corrispondenti nomi di discontinuità di prima, seconda o terza specie, anche ai punti di accumulazione di Dom(ƒ) in cui ƒ non è definita, ma nei quali i limiti abbiano i comportamenti sopra indicati. Per esempio, le funzioni

non sono definite nell’origine ma sono continue in ogni punto del loro dominio (qui inteso, come sinonimo di insieme di definizione). Per poter dire che le tre funzioni hanno rispettivamente una discontinuità di prima, seconda o terza specie si dovrebbe prolungarne la definizione assegnando a ƒ(0) un valore: nel caso di

che ha limite 1 per x che tende a zero, risulta discontinua se ƒ(0) ≠ 1. L’insieme dei punti di discontinuità di una funzione è sempre di tipo F_σ (unione di un’infinità numerabile di chiusi: → Borel, insiemi di). Per esempio, non esistono funzioni che siano discontinue sull’insieme degli irrazionali (insieme di tipo Gδ), mentre la funzione ƒ definita da ƒ(x) = 0 se x è irrazionale, ƒ(x) = 1/q se x = p /q ∈ Q è discontinua solo sui razionali (che è appunto un insieme di tipo F_σ).