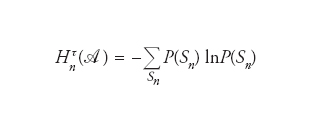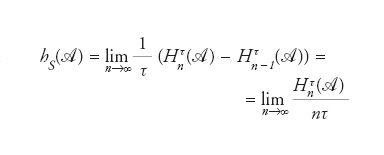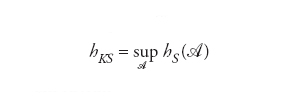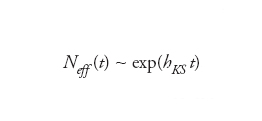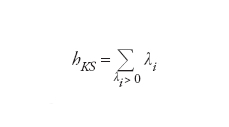entropia di Kolmogorov-Sinai
entropia di Kolmogorov-Sinai
Consideriamo una sequenza xτ1,xτ2,xτ3,..., con xτϚ=x(jτ), ottenuta campionando una traiettoria generata da una condizione iniziale xτ0=x(0) e si introduca una partizione A dividendo lo spazio delle fasi Ω in elementi disgiunti a1,a2,...,aΜ tali che l’unione di tutti gli elementi sia l’intero spazio delle fasi. In questo modo per ogni condizione iniziale si ha una successione di numeri interi i1,i2,... corrispondenti alle celle occupate dalla traiettoria al tempo τ,2τ, ..., ossia se xτϚ∈aϰ allora iϚ=k. In analogia con la teoria dell’informazione, si può definire l’entropia delle successioni Sν di lunghezza n (per es., se M=2 allora per n=2 si hanno le quattro possibili S2 [1;1];[1;2]; [2;1] e [2;2]) con la
dove la probabilità P(Sν) è ottenuta dalla frequenza con cui la successione di simboli Sν compare nella sequenza (arbitrariamente lunga) i1, i2, ... A partire da essa si introduce poi l’entropia di Shannon
nτ Il valore di τ, almeno a livello concettuale, non è essenziale. Prendendo l’estremo superiore su tutte le possibili partizioni A si ottiene l’entropia di Kolmogorov-Sinai hΚΣ
In alcuni sistemi esiste una particolare partizione, detta generante, tale che dalla successione i1,i2, ...,iΝ è possibile risalire alla condizione iniziale x(0) con precisione arbitraria al crescere di N. In una partizione generante l’entropia di Shannon coincide con l’entropia di Kolmogorov-Sinai. Nei casi (tipici) in cui non esiste una partizione generante, l’estremo superiore nell’espressione data per l’entropia di Shannon si ottiene prendendo partizioni costituite da cellette regolari di lati ε con ε→0. Data una partizione sufficientemente accurata, il numero di successioni effettivamente osservate cresce esponenzialmente con il tempo t=nτ
Con ‘effettivamente osservate’ si intende che l’insieme di queste successioni nel limite τ→∞ ha probabilità 1. L’entropia di Kolmogorov-Sinai è strettamente connessa con gli esponenti di Lyapunov λι. È stato dimostrato da Yakov B. Pesin che hΚΣ è la somma degli esponenti di Lyapunov positivi
→ Caos deterministico; Sistemi dinamici. Origini e sviluppi