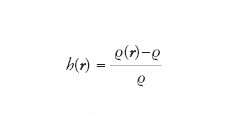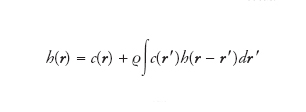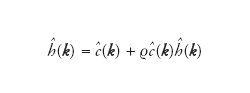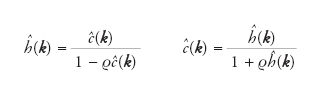equazione esatta di Ornstein-Zernike
equazione esatta di Ornstein-Zernike
Relazione introdotta da Leonard S. Ornstein e Frederick Zernike nel 1914 e utilizzata in meccanica statistica ‒ in particolare nella teoria molecolare dei fluidi ‒ per determinare le funzioni di correlazione corrispondenti a determinate fluttuazioni nella densità di un materiale. Per meglio comprendere la derivazione dell’equazione di Ornstein-Zernicke, è utile introdurre una funzione h(r) che misuri lo spostamento relativo della densità ϱ(r) in un punto r∈ℝ3 dal suo valore medio ϱ. . Si pone quindi
e si osserva che tale grandezza può essere considerata una misura della correlazione totale tra i punti 0 e r di ℝ3 (o se si preferisce tra i costituenti del materiale che occupano le posizioni 0 e r di ℝ3). È allora naturale considerare in prima approssimazione la funzione h(r) come risultato della addizione di due distinti contributi: il primo derivante dalla correlazione diretta tra i punti 0 e r e misurato dalla funzione di correlazione c(r), il secondo determinato invece dalla sovrapposizione delle correlazioni tra i punti 0 e r′ e r′, r di ℝ3. Più precisamente, l’equazione esatta di Ornstein e Zernike è data dalla formula
da interpretarsi come definizione della stessa funzione h(r). L’integrale esprime appunto la sovrapposizione delle correlazioni. Poiché si tratta del prodotto di convoluzione tra le funzioni c(r) e h(r), considerando la trasformata di Fourier di entrambi i membri dell’equazione otteniamo
ovvero
Evidentemente le funzioni hˆ(k) e cˆ(k) non sono determinate dalla sola equazione di Ornstein e Zernike e a questo fine si rende necessaria una ulteriore relazione, detta di chiusura.
→ Liquidi