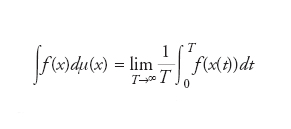ergodicita
ergodicità
Il concetto di ergodicità è stato introdotto da Ludwig Boltzmann nel 1887 nell’ambito dei suoi studi sui fondamenti microscopici della meccanica statistica (e della termodinamica) nella forma di un’ipotesi (detta appunto ipotesi ergodica) sulla densità delle traiettorie nello spazio delle fasi di un ensemble statistico. In effetti, l’orbita esatta nello spazio delle fasi Γ di un sistema statistico classico dotato di N gradi di libertà è ottenuta come soluzione delle equazioni del moto di Hamilton ed è ovviamente unidimensionale. Per moti non strettamente periodici, nel corso del tempo questa traiettoria ricoprirà approssimativamente tutta la superficie (n−1)-dimensionale determinata dalla condizione di conservazione dell’energia. Nel caso dell’ipotesi ergodica, tale osservazione è all’origine della richiesta che ogni punto dello spazio delle fasi permesso dalla conservazione dell’energia sia arbitrariamente vicino a una traiettoria effettiva del sistema nel corso di un intervallo di tempo sufficientemente lungo. I sistemi che soddisfino tale postulato sono detti sistemi ergodici, quelli le cui traiettorie non si avvicinano a una regione dello spazio delle fasi non-ergodici. Una delle principali conseguenze di tale ipotesi è l’indipendenza del valore delle quantità macroscopiche dal metodo di calcolo: considerata una quantità microscopica, la sua media temporale e quella di ensemble (ovvero rispetto a una misura stazionaria sullo spazio delle fasi) coincidono per tutte le funzioni regolari f(x) definite sullo spazio delle fasi. Più precisamente
dove il membro di sinistra è appunto la media della funzione f rispetto alla misura invariante μ(x) e x(t) una qualunque orbita del sistema. La media è definita su un opportuno sottospazio dello spazio delle fasi, per es. come accennato in precedenza le ipersuperfici a energia costante nel caso dell’ensemble canonico. Il calcolo di una media di ensemble è sempre possibile una volta fissato l’ensemble stesso, mentre il calcolo di una media temporale presuppone la conoscenza delle orbite e dunque di una soluzione delle equazioni del moto. Grazie all’ipotesi ergodica questo formidabile ostacolo può quindi essere aggirato. Il passaggio di un sistema dinamico da un regime nel quale l’ipotesi ergodica è soddisfatta a uno nel quale non lo è più è detto rottura della ergodicità.
→ Caos deterministico; Frattali; Irreversibilità; Sistemi dinamici. Origini e sviluppi; Simulazioni dei processi fisici mediante calcolatore; Vetri: fenomeni di non equilibrio