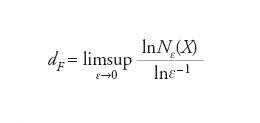geometria frattale
geometria frattale
Appellativo che si riferisce alle proprietà geometriche degli insiemi frattali e al loro studio. Il concetto di insieme frattale è stato originariamente introdotto da Benoît B. Mandelbrot per descrivere insiemi di punti dotati di dimensione di Hausdorff dH non intera. È questa una generalizzazione dell’ordinario concetto di dimensione spaziale. Con l’evolversi della teoria è stato introdotto il concetto di dimensione frattale, fondato sull’osservazione che il numero di sfere necessario a riempire una figura geometrica regolare (per es., nello spazio euclideo tridmensionale) sarà proporzionale al volume, ovvero a una lunghezza L elevata alla potenza 3 (la dimensione dello spazio ambiente). Se la figura è ‘frastagliata’ il numero di sfere necessario a ricoprirla e dunque anche la dimensione stessa potrebbero essere minori. È dunque lecito aspettarsi che estraendo il logaritmo di tale numero sia possibile ottenere una definizione alternativa di dimensione, coincidente con quella ordinaria nel caso di oggetti geometrici sufficientemente ‘lisci’. Formalmente, siano X un sottoinsieme limitato di uno spazio metrico M e per ogni ε>0 sia appunto N (X) il più piccolo numero di palle di raggio ε necessarie a ricoprire X. Si definisce dimensione frattale (o anche capacità e dimensione di Mandelbrot o di Shnirel’man-Kolmogorov) di X il numero
Notiamo che per ogni X si ha dH(X)≤dF(X); un insieme X può dunque avere dimensione di Hausdorff nulla e dimensione frattale diversa da zero, proprietà che rende quest’ultima preferibile. In un gran numero di casi è anche possibile caratterizzare un frattale facendo uso del concetto di (quasi)-autosimilarità. Intuitivamente, scegliendo una porzione comunque piccola di un frattale F e dilatandola fino a portarla alle dimensioni originarie di F si ottiene una figura coincidente in un senso opportuno con F stesso.
→ Frattali; Materia soffice; Turbolenza