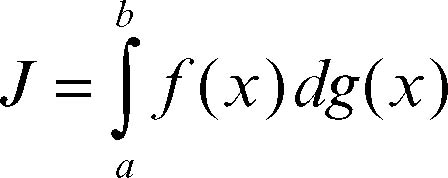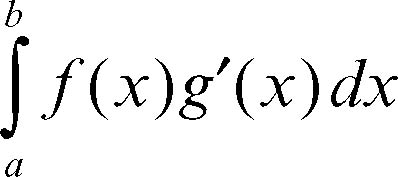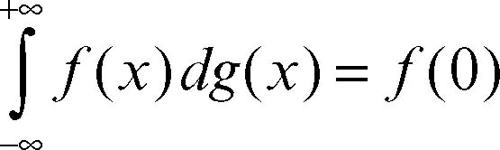Riemann-Stieltjes, integrale di
Riemann-Stieltjes, integrale di
Riemann-Stieltjes, integrale di generalizzazione del concetto di integrale definito ottenuta sostituendo alla variabile d’integrazione una opportuna funzione. Si considerino in un intervallo [a, b] una funzione ƒ(x) limitata e una funzione g(x) monotòna, per esempio crescente. Scelta una suddivisione dell’intervallo mediante una successione di punti {xk} con a = x0 < x1 < ... < xn = b, e detti mk e Mk rispettivamente gli estremi inferiore e superiore di ƒ(x) in [xk−1, xk], si costruiscono le somme integrali per difetto
e per eccesso
Se al tendere a zero della massima lunghezza δ degli intervalli [xk−1, xk] le somme per difetto e quelle per eccesso ammettono lo stesso limite J, la funzione ƒ(x) si dice integrabile secondo Riemann-Stieltjes rispetto alla funzione g(x), e si scrive
Si può poi estendere la definizione all’intervallo (−∞, +∞). Se g(x) è di classe C 1, l’integrale coincide con
e in particolare se g(x) = x esso si riduce all’integrale di → Riemann. Nel caso generale si ottiene una generalizzazione, che include le misure su R. Per esempio, se g(x) = Y(x) (con Y funzione di → Heaviside, cioè Y(x) = 1 per x > 0, Y(x) = 0 per x < 0) e ƒ(x) è continua nell’origine si ha
per cui l’integrale rappresenta la distribuzione δ di → Dirac.