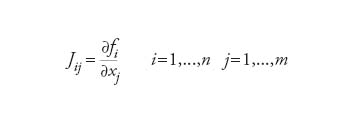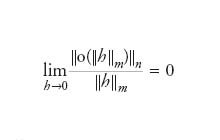matrice jacobiana
matrice jacobiana
Generalizzazione al caso di funzioni di più variabili a valori vettoriali del concetto di derivata di una funzione scalare g:ℝ→ℝ. Più precisamente, si chiama matrice jacobiana J di una funzione (derivabile) f:ℝμ→ℝν la matrice definita dalla formula
formula.
La i-esima riga della matrice jacobiana è dunque composta dalle componenti del vettore gradiente della i-esima componente di f, ovvero dalle sue derivate parziali in ciascuna direzione xξ. Per f sufficientemente regolare, a partire da J è possibile calcolare la parte lineare della variazione di f(x) per effetto di uno spostamento infinitesimo h: indicando con ∣∣ . ∣∣μ una norma in ℝμ, si ha
[2] f(x + h)−f(x) = Jh + o(∣∣h∣∣μ)
dove Jh∈ℝν è il prodotto riga per colonna della matrice J con il vettore h∈ℝμ e
[3] formula.
Si presenta qui una distinzione fondamentale rispetto al caso scalare: l’esistenza di J, detta derivabilità, non è in realtà sufficiente a garantire che la [2] sia verificata. Se questo è il caso, f è detta differenziabile. Ma se J esiste e inoltre ciascuna componente Jιξ è continua, allora f è differenziabile. Di fondamentale importanza è il caso f:ℝν→ℝν. La matrice jacobiana è allora quadrata e il suo determinante detJ (determinante jacobiano) è definito (e sarà una funzione di x∈ℝν). Uno dei più importanti teoremi dell’analisi matematica classica, il teorema della funzione inversa, afferma che una funzione f:ℝν→ℝν è invertibile in un intorno opportuno di un punto x0∈ℝν se detJ calcolato in x0 è diverso da zero. Infine, il valore assoluto del determinante jacobiano caratterizza la dilatazione (o contrazione) di un volume infinitesimo come risultato di una trasformazione di coordinate. Tale proprietà trova applicazione nel calcolo di integrali di volume con la tecnica del cambiamento di variabili.