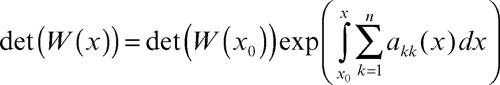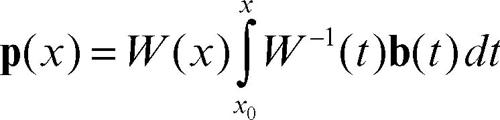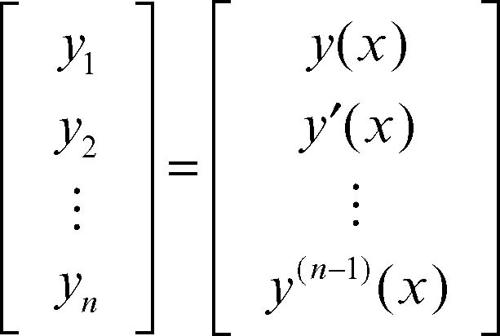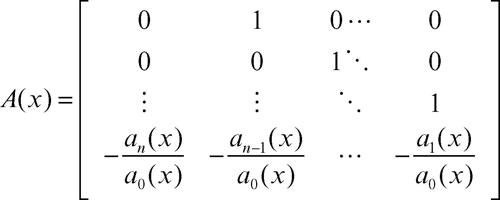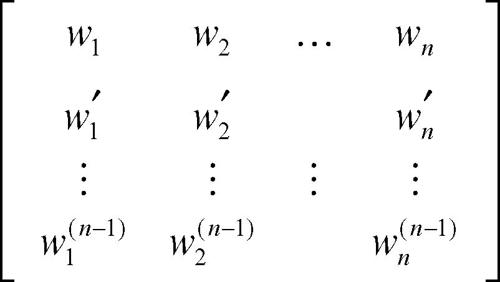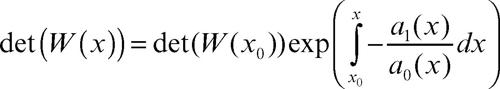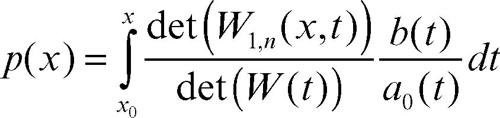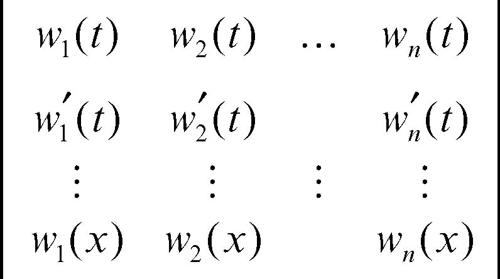matrice wronskiana
matrice wronskiana
matrice wronskiana per un sistema omogeneo y′ = A(x)y di n equazioni differenziali ordinarie lineari nell’incognito vettore y(x), è una matrice W(x) le cui colonne sono costituite da n soluzioni linearmente indipendenti wk(x), 1 ≤ k ≤ n, del sistema stesso. Si supponga che la matrice dei coefficienti A(x) sia continua in un intervallo [a, b]. Se det(W(x)) ≠ 0 in [a, b], e quindi la matrice è invertibile, il sistema di vettori viene detto fondamentale, e l’integrale generale del sistema differenziale è dato da W(x)c, con c vettore costante arbitrario. In realtà, si può verificare la validità della condizione det(W(x)) ≠ 0 anche in un solo punto x0 ∈ [a, b], perché vale la relazione
(→ Jacobi, teorema di).
La matrice wronskiana soddisfa l’equazione differenziale W′′(x) = A(x) ⋅ W(x), il che permette di identificare i coefficienti del sistema, ove incogniti, a partire da n soluzioni linearmente indipendenti; vale infatti la relazione: A(x) = W′′(x) ⋅ W−1(x).
La conoscenza di una matrice wronskiana fondamentale consente di scrivere anche una soluzione particolare p(x) del sistema completo y′ = A(x)y + b(x). Ponendo infatti y(x) = W(x)q(x) e sostituendo, si ricava
Il metodo, dovuto a Eulero, viene detto metodo di variazione delle costanti in quanto l’espressione W(x)q(x) appare ottenuta da quella dell’integrale generale W(x)c dell’omogenea, sostituendo al vettore costante c la funzione vettoriale q(x).
Un’equazione di ordine n, a0(x)y(n) + a1(x)y(n−1) + ... + an(x)y = b(x) si trasforma in un sistema introducendo il vettore
le cui componenti sono l’incognita e le sue derivate fino all’ordine n − 1. La corrispondente matrice dei coefficienti ha tutti elementi nulli, salvo avere degli 1 al di sopra della diagonale principale, e avere nell’ultima riga i coefficienti dell’equazione divisi per il coefficiente dominante a0(x), che si deve supporre diverso da zero:
La matrice wronskiana assume quindi la forma
in cui la prima riga contiene n integrali particolari e le successive le loro derivate fino all’ordine n − 1. Il teorema di Jacobi diventa
(teorema di Liouville sul wronskiano) e il metodo di variazione delle costanti fornisce una soluzione p(x) dell’equazione completa nella forma
dove det(W(t)) è il determinante wronskiano e det(W1,n(x, t)) è il determinante seguente:
ottenuto sostituendo nell’ultima riga della matrice wronskiana W(t) la prima riga valutata in x.