monoide
Enciclopedia on line
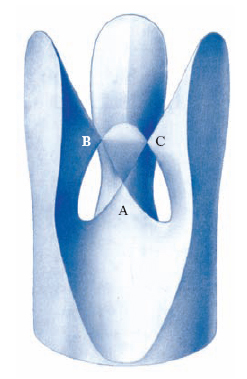
Superficie algebrica irriducibile d’ordine n, avente un punto P di molteplicità n−1; essa è razionale e le sue equazioni parametriche razionali si ottengono intersecandola con una retta generica per P, cioè riferendola birazionalmente alla stella di rette per P. L’equazione cartesiana, quando P coincida con l’origine delle coordinate, è Ψn(x, y, z)+Ψn–1(x, y, z)=0 ove Ψn, Ψn–1 sono polinomi omogenei di grado n, n−1. Il concetto di m. si estende alle ipersuperfici degli iperspazi. Il più semplice esempio di m. è fornito da una quadrica (n=2 e P un qualunque punto semplice); un altro esempio è dato da una superficie cubica (v. fig.) che possieda uno o più punti doppi.