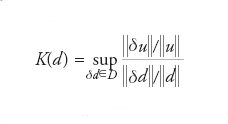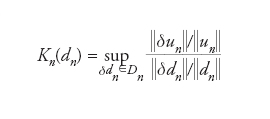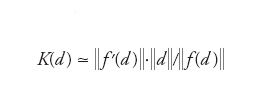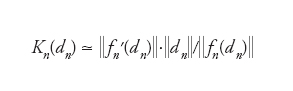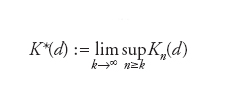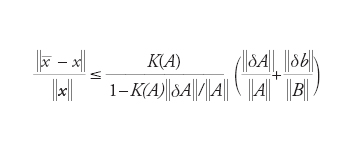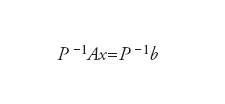numero di condizionamento
numero di condizionamento
Si consideri il problema di trovare u tale che F(u,d)=0, dove d è l’insieme dei dati da cui dipende la soluzione e F esprime la relazione (detta anche legge funzionale) che lega u a d. Supponiamo che il modello matematico F(u,d)=0 sia ben posto, ovvero che esista un’unica soluzione u e questa dipenda con continuità dai dati d. Questo vuol dire che se d e d* rappresentano due possibili insiemi di dati e ∂δd=d*−d la loro differenza, u, u* e δu=u*−u le corrispondenti soluzioni e la loro differenza, allora diciamo che il modello matematico F(u,d)=0 è ben posto in corrispondenza del dato d se per ogni ε>0 esiste K(ε,δd)>0 tale che ∣∣∂δd∣∣〈ε implica ∣∣−δu∣∣≤K(ε,d)∣∣∂δd∣∣. Abbiamo indicato con lo stesso simbolo ∣∣∙∣∣ delle norme opportune (non necessariamente le stesse) per l’insieme dei dati e quello delle soluzioni. Se d≠0, il numero di condizionamento del modello matematico è definito come
dove D rappresenta l’insieme di tutte le perturbazioni non nulle ammissibili dei dati. Se ora consideriamo il modello numerico Fn(un,dn)=0, anziché quello matematico, possiamo procedere esattamente come abbiamo fatto sopra ed associare un numero di condizionamento anche al modello numerico, definito come
dove Dn rappresenta l’insieme di tutte le perturbazioni non nulle ammissibili dei dati per il problema numerico. Supponiamo ora che la soluzione u del modello matematico si possa esprimere esplicitamente in funzione dei dati d come u=F(d) e analogamente si abbia un=Fn(dn) per il modello numerico. Se le leggi f e fn sono differenziabili, applicando uno sviluppo di Taylor arrestato al primo termine si ottengono le seguenti stime per K(d) e Kn(dn):
e, analogamente,
Se l’insieme Dn coincide con l’insieme D possiamo definire il numero di condizionamento asintotico del modello numerico come
A titolo di esempio si consideri il problema di calcolare la soluzione del sistema lineare quadrato non singolare Ax=b. In tal caso il numero di condizionamento del modello matematico risulta essere K(A)=∣∣A∣∣∙∣∣A−1∣∣ e viene detto numero di condizionamento della matrice A, dove ∣∣∙∣∣ rappresenta una qualsiasi norma matriciale. K(A) entra in gioco nella risoluzione dei sistemi lineari come fattore di amplificazione degli errori sui dati e, nel caso si voglia risolvere il sistema lineare con metodi iterativi, è responsabile della velocità di convergenza del metodo stesso alla soluzione del sistema lineare. In particolare, se indichiamo rispettivamente con ∂δA e δ∂b delle perturbazioni sulla matrice A e sul termine noto b del sistema lineare, tali che ∣∣∂δA∣∣∙∣∣A−1∣∣〈1, la soluzione ottenuta risolvendo il sistema perturbato (A+δ∂A)x_=b+δb soddisfa la stima a priori
Questa stima mette in evidenza il fatto che il numero di condizionamento di una matrice è un indicatore di quanto gli errori sui dati si amplifichino nel risolvere il sistema lineare dato e si riflettano sull’errore tra la soluzione del sistema perturbato e la soluzione del sistema originario. Una matrice si dice ben condizionata se K(A) è prossimo a uno, mentre A si dice mal condizionata se K(A)>>1. Un esempio notevole di matrice mal condizionata è la matrice di Hilbert H con Hij=1/(i+j−1), per i,j=1,...,n. Tale matrice è simmetrica, non singolare e ha un numero di condizionamento che cresce esponenzialmente con n, in particolare K(H)≃0,01e3,5n. Qualora si utilizzi il metodo del gradiente coniugato per la risoluzione del sistema lineare dato, si ottiene che dopo n iterazioni il rapporto
(dove ∣∣x∣∣A=√____xTAx) è controllato da 2cn/(1+c2n) con c=(√______K(A)−1)/(√______K(A)+1). Da questa stima si deduce che tanto più K(A) è prossimo a uno, ovvero tanto più la matrice A è ben condizionata, tanto più è veloce la convergenza del metodo alla soluzione x. Una tecnica per ovviare al problema di sistemi mal condizionati (ovvero sistemi le cui matrici sono mal condizionate) consiste nel sostituire al sistema Ax=b un sistema equivalente
detto sistema precondizionato, in cui P è un’opportuna matrice invertibile (semplice da costruire e detta precondizionatore) con la proprietà che K(P−1A)〈〈K(A). Un precondizionatore efficiente può essere costruito o mediante tecniche algebriche (per es., può essere ottenuto da una fattorizzazione incompleta di A) o mediante tecniche differenziali qualora il sistema lineare da risolvere derivi dall’approssimazione di un problema differenziale. → Computazionali, metodi