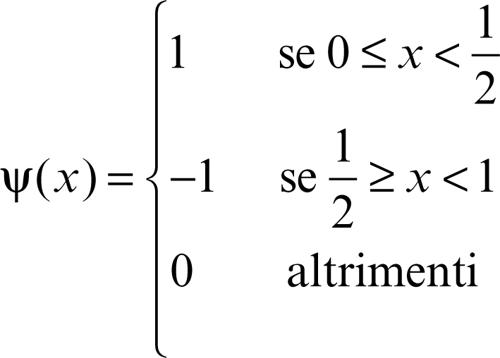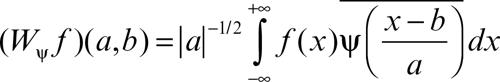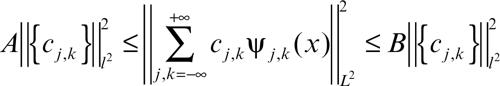ondine

ondine

ondine (in inglese wavelets) famiglia di funzioni che consentono di eseguire una analisi di tipo Fourier assai generale e versatile per le applicazioni (→ Fourier, trasformazione di). Un’ondina fornisce un sistema ortonormale completo in L²(R) (→ spazio L²(Ω)).

Si consideri una funzione ψ(x) ∈ L²(R), detta ondina madre, e si costruiscano con essa le traslate e dilatate diadiche ψ_j,_k(x) = 2^j/2ψ(2^jx − k). Se ψ ha norma unitaria, anche ||ψ_j,k(x)|| = 1. L’ondina ψ è detta ortonormale se le ψ_j,_k(x) formano un sistema ortonormale completo in L²(R), cioè se risulta (ψ_j,_k(x), ψ_l,_m(x)) = δ_j,_l δ_k,_m, dove δ è il simbolo di → Kronecker e (u, ν) è il prodotto scalare in L²(R). La completezza del sistema significa che ogni funzione ƒ ∈ L²(R) può essere espressa da una serie

dove i coefficienti c_j,_k sono dati dai prodotti scalari c_j,_k = (ƒ, ψ_j,_k). L’esempio più semplice è dato dall’ondina di Haar, dal nome del matematico ungherese A. Haar, che per primo introdusse le ondine nel 1909:

I coefficienti possono essere anche ottenuti a partire dalla cosiddetta trasformata ondina di ƒ,

risultando c_j,_k = (W_ψƒ )(k/2^j, 1/2^j). Le serie di ondine e le trasformate ondine risultano così strettamente collegate, mentre nel caso delle serie e delle trasformate di Fourier le due nozioni sono alternative, l’una escludendo l’altra.

In generale, non si richiede tuttavia che ψ sia un’ondina ortonormale, essendo sufficiente che le funzioni {ψ_j,_k(x)} costituiscano una base di Riesz, cioè che le loro combinazioni lineari siano dense in L²(R) ed esistano due costanti A, B, con 0 < A ≤ B < +∞, per cui risulti

per ogni successione {c_j,_k} ∈ l ² (a quadrato sommabile). Queste disuguaglianze generalizzano l’uguaglianza di Parseval (→ Parseval, identità di), cui si riducono se A = B. Le funzioni ψ sono scelte in genere tra le funzioni spline di un opportuno ordine m, in modo da consentire l’analisi multirisoluzione (mra), cioè l’approssimazione di L²(R) mediante sottospazi che “catturano” dettagli sempre più fini. La mra è importante nelle applicazioni all’analisi di segnali e alla compressione di immagini.