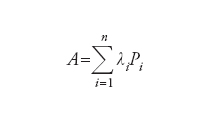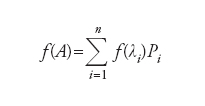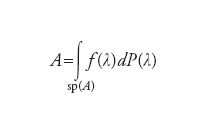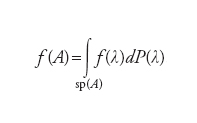operatori hermitiani

operatori hermitiani

Sia A:ℋ→ℋ un operatore lineare continuo (limitato) di uno spazio di Hilbert in sé e siano (∙,∙) il prodotto scalare di ℋ e ∣∣∙∣∣ la norma da esso indotta. Fissato y∈ℋ, la formula (Ax,y) definisce un funzionale lineare, cui corrisponde per il teorema di Riesz un unico elemento z∈ℋ tale che (x,z)=(Ax,y). L’operatore aggiunto (coniugato hermitiano) A* di A è definito dalla formula z=A*y e soddisfa l’uguaglianza (Ax,y)=(x,A*y). Notiamo che se ∣∣A∣∣=sup∣∣Ax∣∣/∣∣x∣∣〈∞, allora ∣∣A∣∣=∣∣A*∣∣. Un operatore lineare limitato A su uno spazio di Hilbert ℋ è detto hermitiano (o autoaggiunto) se A=A*. Un esempio elementare ma importante di operatori hermitiani è costituito dalle proiezioni ortogonali, ovvero operatori tali che P=P²=P*. Se A:Vⁿ→Vⁿ è un operatore hermitiano di uno spazio di Hilbert di dimensione n (ovvero ℂⁿ dotato del prodotto scalare ordinario) in sé, allora esistono proiezioni P_i e λ_i∈ℝ (gli autovalori di A, non tutti necessariamente distinti) tali che

formula.

Gli operatori P_i proiettano su sottospazi unidimensionali ortogonali tra loro (P_iP_j=0 se ifij): ogni matrice hermitiana ammette una base ortogonale nella quale è diagonale. Notiamo che se Ax=λx (ovvero x è un autovettore con autovalore λ) allora λ(x,x)= (Ax,x)=(x,Ax)=(x,λx)=λ_(x,x) e λ è reale. Data infine una funzione f: ℝ→ℝ, è possibile definire un nuovo operatore hermitiano

[2] formula.

Questo insieme di enunciati va sotto il nome di teorema spettrale per matrici e la sua generalizzazione al caso di dimensione infinita è stato uno dei grandi successi dell’analisi funzionale. La principale differenza con il caso di dimensione finita è che lo spettro di A non è necessariamente discreto e composto dai soli autovalori: questi ultimi possono per così dire addensarsi fino a formare un continuo. A questo fenomeno corrisponde, approssimativamente, la trasformazione della serie in [1] in un integrale

[3] formula

dove dP(λ) è detta misura spettrale. La definizione del concetto di funzioni di un operatore hermitiano resta analoga ed è alla base del cosiddetto calcolo funzionale:

formula.

[4] formula.

Ricordiamo infine che il concetto di operatore hermitiano può essere esteso anche a operatori non limitati (ovvero non continui) e con esso il teorema spettrale e il calcolo funzionale.

→ Supersimmetria