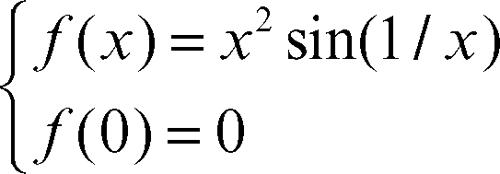punto stazionario
punto stazionario
punto stazionario per una funzione reale di una variabile ƒ(x), derivabile, è un punto x0 in cui ƒ′ (x0) = 0. Questa condizione significa che la retta tangente è parallela all’asse delle ascisse. Analogamente, per funzioni differenziabili di più variabili sono detti stazionari i punti in cui gradƒ = 0 (dove gradƒ indica il → gradiente della funzione scalare ƒ ); il significato geometrico di questa condizione è del tutto analogo a quello di una funzione in una variabile, riferito però all’(iper)piano tangente nel punto. Se una funzione è differenziabile, in una o più variabili, e il punto x0 è interno a Dom(ƒ ), la condizione di stazionarietà è necessaria affinchè il punto in esame sia un → punto estremante (massimo o minimo), ma non è sufficiente, potendosi trattare di un → flesso o di un punto di → sella (→ matrice hessiana), o di altra configurazione più complessa. Per esempio, il punto x0 = 0 è di stazionarietà per le funzioni y = xn per ogni n > 1, n ∈ N, ma è di minimo solo se n è pari, di flesso se n è dispari. Analogamente le funzioni z = xn + ym hanno un punto di stazionarietà nell’origine per n, m > 1, ma solo se n e m sono entrambi pari esse hanno un minimo, mentre se anche uno solo dei due esponenti è dispari il grafico attraversa il piano tangente z = 0. La funzione così definita:
ha un punto di stazionarietà nell’origine, ma il suo grafico attraversa infinite volte l’asse x in ogni intorno dell’origine. Tuttavia si può avere un estremo anche se il punto non è stazionario, nel caso non siano soddisfatte le altre ipotesi. Per esempio, il punto x0 = 0 è di minimo per ƒ(x) = |x| in [−1, 1] (manca la differenziabilità) e per ƒ(x) = x in [0, 1] (x0 non è interno all’intervallo).