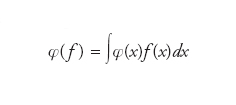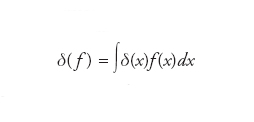spazio delle distribuzioni

spazio delle distribuzioni

Una generalizzazione del concetto classico di spazio di funzioni, la cui necessità si presenta in molti problemi fisici e matematici. Il concetto di distribuzione (o anche funzione generalizzata) permette di esprimere in maniera rigorosa concetti quali per es. la densità di un punto materiale o l’intensità di una sorgente istantanea. D’altro canto, il concetto di distribuzione riflette il fatto che in realtà una quantità fisica non può essere misurata in un punto: solo valori medi in un intorno di esso sono accessibili all’esperienza, una situazione per l’appunto convenientemente descritta facendo uso di distribuzioni di valori possibili. Formalmente, una distribuzione è definita come un funzionale lineare continuo φ su un qualche spazio vettoriale topologico F di funzioni (dette funzioni test) sufficientemente regolari: (a) φ(f₁+f₂)=φ(f₁)+φ(f₂) e φ(λf)=λφ(f) per ogni f₁,f₂,f∈F e λ∈ℂ; (b) φ(f_i)→φ(f) se f_i→f nella topologia di F. In altri termini, uno spazio di distribuzioni è definito come spazio duale (topologico) F* di un qualche spazio vettoriale topologico di funzioni F sufficientemente regolari. Poiché dalla relazione G⊂F (G si intende dotato della topologia indotta da F) segue in generale che G*⊂F*, è evidente che considerando spazi di funzioni test più regolari si estende la classe di distribuzioni considerata. Un importante esempio di spazio di funzioni test è costituito dallo spazio D(O) delle funzioni infinitamente differenziabili su un aperto connesso O⊂ℝⁿ con supporto compatto (chiuso e limitato) contenuto in O, dotato di un’opportuna topologia. Spesso il termine spazio di distribuzioni è utilizzato per indicare lo spazio D(O)*. Il più semplice esempio di distribuzioni (in D(O)*) è fornito dalle funzioni localmente integrabili φ e

per ogni f∈D(O). In questo senso, funzioni ordinarie come le funzioni integrabili sono distribuzioni. Viceversa, se una distribuzione può essere definita tramite la formula precedente in termini di funzioni localmente integrabili essa è detta regolare e singolare in caso contrario. Un importante esempio di distribuzione singolare su ℝⁿ è la δ di Dirac, definita dalla relazione δ(f)=f(0) per f∈D(ℝⁿ). Talvolta si scrive anche

e per questa ragione si usa affermare che la δ di Dirac è una funzione nulla ovunque tranne che nell’origine di ℝⁿ, dove vale +∞. È quindi chiaro che in generale una distribuzione può non essere definita in un singolo punto.

→ Equazioni funzionali