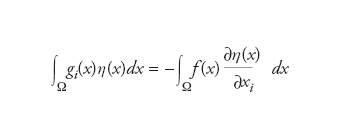spazio di Sobolev

spazio di Sobolev

Per trattare problemi di equazioni differenziali ci si pone in spazi di funzioni che devono ammettere derivate in un qualche senso, anche debole, e devono essere completi per poter passare al limite nel processo di approssimazione. Negli spazi di Sobolev si definiscono le derivate in un senso distribuzionale, cioè mediante integrazione con funzioni test η. Sia Ω un aperto dello spazio a N dimensioni ℝ^N. Si dice che una funzione g_i in L¹(Ω) è la derivata parziale rispetto alla variabile x_i di una funzione f di L¹(Ω) se, per ogni funzione test η regolare (cioè che ammette derivate parziali nel senso puntuale) e nulla al bordo (più precisamente, a supporto compattamente contenuto in Ω), si ha

Se questo avviene per tutte le variabili x_i si dice che la funzione vettoriale g₁, ..., g_N è il gradiente (in senso debole) della funzione f e che f sta nello spazio di Sobolev W^1,1(Ω).

→ Convessità