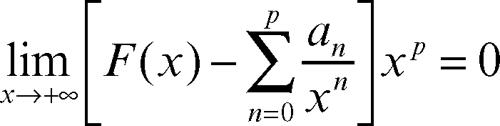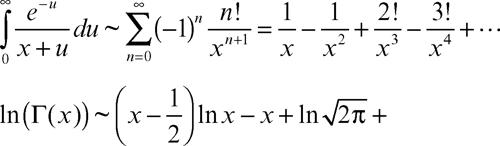sviluppo asintotico
sviluppo asintotico
sviluppo asintotico (di una funzione) serie di funzioni che, pur non convergendo in alcun punto, fornisce informazioni atte allo studio asintotico della funzione sviluppata. Precisamente, la serie
fu chiamata da Poincaré rappresentazione asintotica di una funzione F(x) nel caso in cui, per ogni fissato p ≥ 0, risulti
Se la serie considerata converge a F(x) in un intorno di +∞, è senz’altro un suo sviluppo asintotico, ma i casi interessanti sono proprio quelli in cui la serie non converge. Si scrive allora
Più in generale, si scrive
per indicare che
È possibile manipolare sviluppi asintotici come serie formali, eseguendone la somma, il prodotto, il quoziente, la composizione, come se convergessero, sotto ipotesi assai larghe. Per esempio:
(da cui la formula di → Stirling);
con B2k numeri di Bernoulli.
In tutti questi casi la serie è a segni alterni, e l’errore che si commette troncandola non supera in modulo il primo termine trascurato, come avviene per le serie convergenti. Per esempio, se si vuole calcolare l’integrale del primo esempio per x = 10 con 3 cifre decimali basterà considerare solo i primi tre addendi, perché 3!/104 < 10−3.
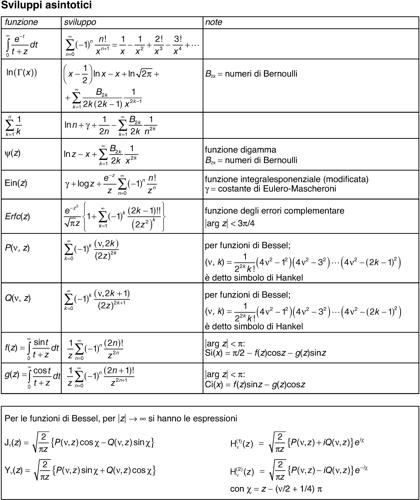
Numerose sono le rappresentazioni asintotiche concernenti le funzioni di → Bessel, le funzioni ipergeometriche e i polinomi ortogonali. Anche la formula di sommazione di → Eulero-Maclaurin fornisce lo spunto per svariati sviluppi asintotici (si veda la tavola degli sviluppi asintotici).