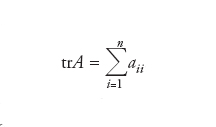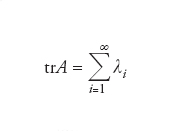traccia
traccia
Nel caso di un operatore lineare (matrice quadrata) di uno spazio vettoriale euclideo n-dimensionale in sé A=∣∣aij∣∣ (con aij numeri complessi e i,j=1,...,n), la traccia di A è definita dalla
Evidentemente, se A e B sono matrici quadrate dello stesso ordine e α,β∈ℂ allora: (a) tr(αA+βB)=αtrA+βtrB (linearità); (b) trAB=trBA; (c) trA*A≥0 (positività). Il simbolo A* indica la matrice coniugata hermitiana di A. Se A è hermitiana (A=A*), trA è uguale alla somma dei suoi autovalori. La generalizzazione del concetto di traccia al caso di spazi vettoriali di dimensione infinita dotati di prodotto scalare (di Hilbert) ℋ si è dimostrata uno strumento fondamentale nello studio delle sottoalgebre dell’algebra degli operatori lineari limitati su di essi B(ℋ). Un primo metodo procede direttamente dalla definizione precedente. Se A è un operatore hermitiano su uno spazio di Hilbert ℋ con spettro discreto e autovalori λi (per es., un operatore compatto) si dirà traccia di A la somma della serie
È importante notare che, a differenza del caso finito-dimensionale, la convergenza della serie non è ovviamente garantita. Se un operatore A ha traccia finita, esso è detto di classe traccia. Per il secondo metodo, il punto di partenza sono invece le proprietà (a), (b), (c): data una sottoalgebra (debolmente chiusa, ovvero di von Neumann) A⊂B(ℋ), si dice traccia (numerica) su A un funzionale tr:A→ℂ che le soddisfi. Una traccia si dirà finita se tr(A*A)〈+∞ per ogni A∈A, semifinita se tr(A*A)=sup{tr(B*B) tali che B∈A, B*B〈A*A e tr(B*B)〈+∞}. L’esistenza o non esistenza di una traccia è una delle più importanti caratteristiche delle algebre di von Neumann e un ingrediente essenziale della loro classificazione. Approssimativamente, l’esistenza di una traccia finita o semifinita su A è infatti equivalente all’esistenza di proiettori in A dotati di particolari proprietà. Sono questi ultimi alla base della distinzione (non ancora una classificazione completa) delle algebre di von Neumann in tre tipi (I, II, III).