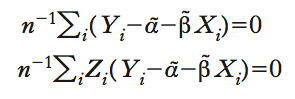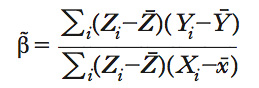variabili strumentali, metodo delle
variabili strumentali, metodo delle
Metodo per stimare in modo consistente (➔ consistenza) i parametri di un modello lineare della forma Y=α+β′X+U quando, a causa dell’endogeneità dei regressori X (➔ endogeno/esogeno), il metodo dei minimi quadrati ordinari (➔ minimi quadrati, metodo dei) produce stime inconsistenti. L’endogeneità può sorgere in diversi casi: nell’omissione di v. rilevanti dal modello, in modelli dinamici con disturbi autocorrelati (➔ autocovarianza), nella causalità simultanea (➔ causalità), e nel caso in cui l’osservazione di uno o più regressori del modello sia soggetta a un errore aleatorio. In tutte queste situazioni, una soluzione al problema dell’inconsistenza dei minimi quadrati ordinari è rappresentata dall’esistenza di una o più v. con la duplice proprietà di essere rilevanti, cioè asintoticamente correlate con il regressore o i regressori endogeni, ed esogeni, cioè asintoticamente incorrelate con l’errore di regressione. Tali v., dette strumenti perché non influenzano direttamente la variabile dipendente Y (➔ dipendente, variabile), se non indirettamente attraverso il loro effetto sui regressori, sono indicate con il vettore Z=(Z1,...ZR). Ipotizzando che le osservazioni siano il frutto di campionamento casuale, le v. s., o ‘strumenti’, in Z sono valide se: E(ZU)=0 (esogeneità degli strumenti), cioè ciascuno strumento Zr è incorrelato con l’errore U,r=1,..., R, o se la matrice E(ZX′) ha rango colonna pieno (rilevanza degli strumenti).
Condizioni di applicabilità
Il metodo delle v. s. è implementabile se il numero di strumenti in Z è almeno uguale al numero di regressori endogeni in X. Un modello con K regressori endogeni e R=K v. s. si definisce esattamente identificato; un modello con K regressori endogeni e R>K strumenti si dice sovraidentificato. Per la discussione dei due casi, ci si limita a considerare la situazione in cui tutti i K covariante endogene in X sono endogeni. Nella situazione in cui (R=K), il metodo delle v. s. si riduce a imporre che i dati soddisfino la condizione di incorrelazione tra gli strumenti e il residuo della regressione. Questa rappresenta il corrispondente empirico della condizione di esogeneità degli strumenti. Nel caso di una sola covariata e un solo strumento (R=K=1), ciò significa trovare i valori ᾶ e β῀ che soddisfano la coppia di equazioni:
da cui si ottengono le stime delle v. s.:
Si noti che lo stimatore β῀ è uguale al rapporto tra la covarianza campionaria tra Z e Y e la covarianza campionaria tra Z e X. Il caso particolare in cui lo strumento è una variabile dicotomica (➔ variabile categorica), cioè una variabile che assume soltanto valore 0 o 1, è noto come stimatore di Wald. ● Nel caso di sovraidentificazione (R>K), il sistema di equazioni (1) ha più equazioni che incognite (compresa l’intercetta) e quindi non ammette soluzioni se gli strumenti sono rilevanti. In tale circostanza, lo stimatore delle v. s. di α e β si ottiene imponendo la condizione che il vettore degli R+1 momenti campionari V(α,β)=n−1Σi=1Zi(Yi−α−β′Xi) si discosti da 0 il meno possibile. Lo stimatore delle v. s. minimizza quindi la distanza quadratica V(α,β)′WV(α,β), dove W è una matrice di pesi simmetrica e definita positiva. A seconda della scelta di W si ottengono stimatori di v. s. diversi: tale metodo è anche detto metodo generalizzato delle v. strumentali.
Proprietà
Derivare le proprietà per campioni finiti di uno stimatore di v. s. è complicato. Sebbene esso sia in generale distorto (non corretto), sotto opportune condizioni esso è consistente e asintoticamente normale con una matrice di varianza asintotica che dipende dalla scelta della matrice di pesi W. Lo stimatore dei minimi quadrati a due stadi (➔ stimatore) è un caso speciale corrispondente alla scelta della matrice di pesi W=(nZ′Z)−1 ed è asintoticamente efficiente (➔ efficienza statistica) quando gli errori di regressione sono omoschedastici e serialmente incorrelati.
Scelta degli strumenti
Il problema della scelta degli strumenti è estremamente importante. Infatti, se questi sono endogeni, cioè correlati con l’errore di regressione, allora lo stimatore delle v. s. è inconsistente. Se gli strumenti sono ‘deboli’, cioè scarsamente correlati con i regressori endogeni, allora non soltanto diminuisce la precisione dello stimatore di v. s., ma può anche aumentare considerevolmente la sua distorsione. Al tempo stesso, i risultati asintotici convenzionali si rivelano di scarsa utilità pratica. La scelta degli strumenti deve essere sorretta da una conoscenza specifica dei meccanismi economici e istituzionali che determinano le variabili osservate. Esistono anche procedure formali di test circa la bontà degli strumenti utilizzati: in particolare, la condizione di rilevanza può essere verificata direttamente attraverso il test di significatività della regressione (detta forma ridotta o regressione del primo stadio), che esprime i regressori endogeni come funzione lineare dei regressori esogeni e degli strumenti. La condizione di esogeneità degli strumenti può invece essere verificata soltanto nel caso di sovraidentificazione, usando il test di Sargan (➔ Sargan, John Denis).