varianza
varianza
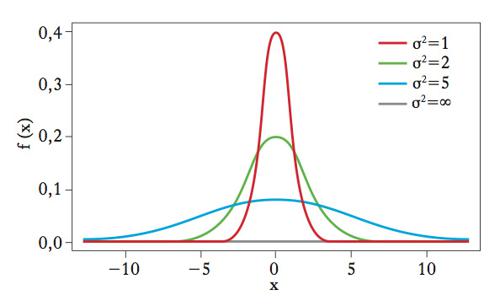
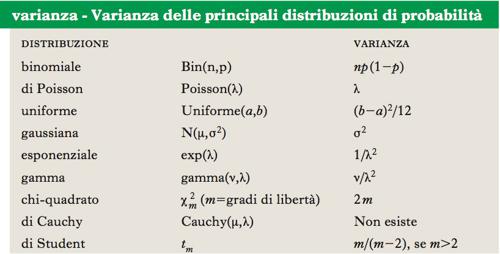
Misura di dispersione di una distribuzione o di una variabile aleatoria. Dato un insieme di n numeri {x1,...xn}, si definisce come loro v. la media dei loro scostamenti quadratici (➔ scostamento) dalla media aritmetica (➔ media), cioè sx2=Σi(xi−x̄)2/n, dove x̄=Σixi/n. Se {x1,...xn} sono i valori possibili di una variabile casuale discreta X (➔ variabile aleatoria) di media μ, si definisce varianza di X la media dello scostamento quadratico di X dalla sua media, cioè Var(X)=E(X−μ)2=Σipi(xi−μ)2, dove il peso pi è uguale alla probabilità che X assuma il valore xi. In questo caso la varianza di X si indica generalmente con il simbolo sx2. Se X è una variabile aleatoria continua, la definizione di v. è analoga, ma la somma è sostituita da un integrale, mentre i pesi sono proporzionali alla densità f della distribuzione (➔ distribuzione di probabilità), tale che Var(X)=ʃ(x−μ)2f(x)dx. Per un insieme di n numeri, o per una variabile casuale discreta che assume un numero finito di valori, la v. esiste sempre finita. Nel caso generale di una variabile aleatoria, condizione sufficiente affinché la v. esista finita è che i primi due momenti della variabile aleatoria esistano finiti. La formula della v, infatti, può essere equivalentemente scritta come Var(X)=E(X)2−μ2, cioè come differenza tra il momento secondo di X e il quadrato della media. Se esiste finita, la v. non è mai negativa ed è uguale a 0 soltanto se X=μ con probabilità 1, cioè, in altre parole, se X è costante. La tabella riassume le varianze delle principali distribuzioni di probabilità. Per ogni costante a, si ha Var(aX)=a2sx2. Se X e Y sono due variabili aleatorie indipendenti, di v. sx2 e sy2, allora si ha Var(X+Y)=sx2+sy2. Se X e Y non sono indipendenti, allora Var(X+Y)=sx2+sy2+2σXY, dove σXY indica la covarianza tra X e Y.