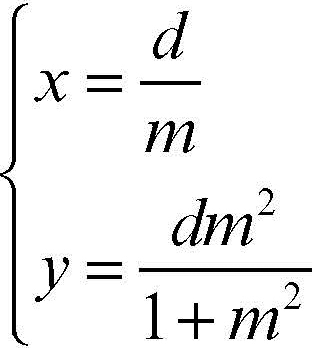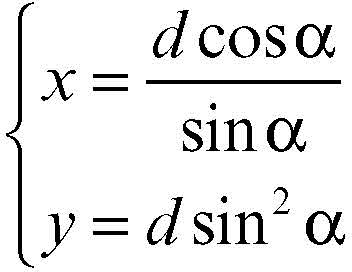Agnesi, versiera di
Agnesi, versiera di
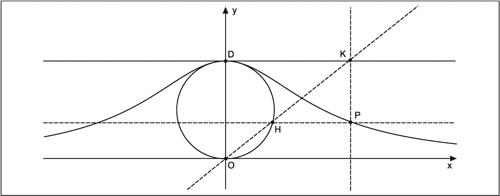
Agnesi, versiera di curva algebrica piana del terzo ordine, definita come particolare luogo geometrico. Per la sua costruzione, si considera un punto H di una circonferenza di diametro OD e si indica con K l’intersezione della retta OH con la tangente in D alla circonferenza. Tracciate da H e K, rispettivamente, la parallela e la perpendicolare alla tangente in D, sia P la loro intersezione. La versiera è il luogo descritto dal punto P al variare del punto H sulla circonferenza.
Introdotto un sistema di riferimento Oxy, la retta per OH ha equazione y = mx, cioè y = tanαx, mentre la circonferenza, il cui diametro è indicato con d, ha equazione x2 + y2 − dy = 0.
La versiera ha equazioni parametriche:
ovvero
ed equazione cartesiana
La versiera è simmetrica rispetto all’asse y e tende asintoticamente all’asse x. La regione illimitata compresa tra la curva e l’asse x ha area finita uguale a 4(. La versiera, normalmente associata al nome di M.G. Agnesi, fu in realtà studiata per la prima volta da F.L. Grandi, che l’aveva chiamata curva con seno verso, cioè «inverso del seno», ma anche «contrario», «nemico». Di qui, versiera (nel senso di «avversaria», dal francese aversier), nome solitamente attribuito alle streghe. In inglese la curva è infatti nota come witch of Agnesi (strega di Agnesi).