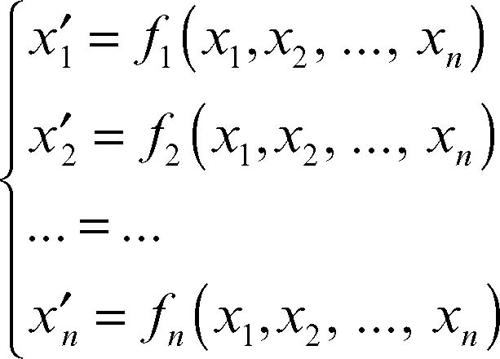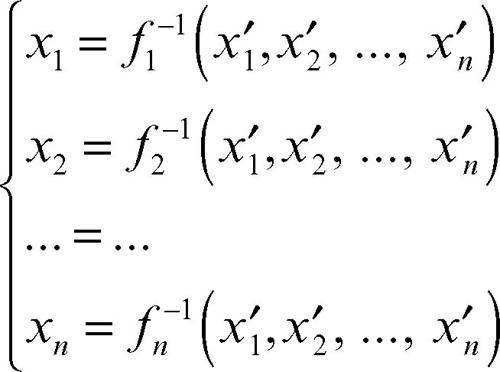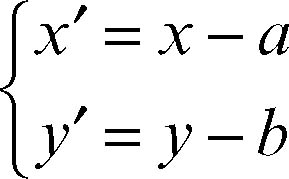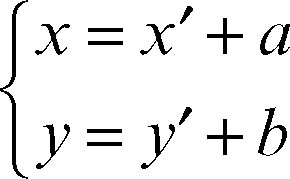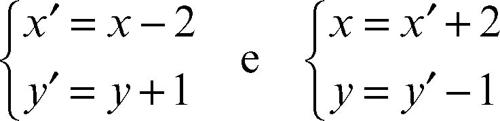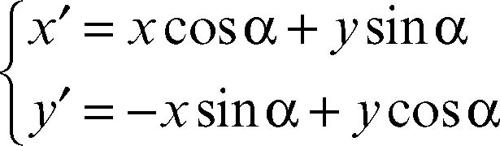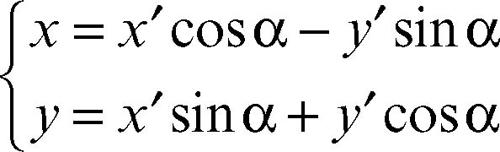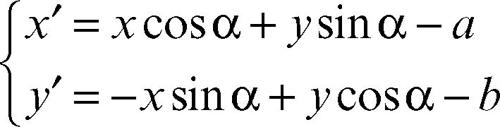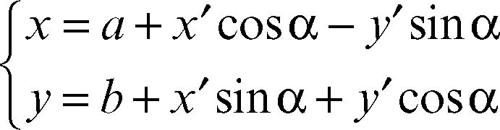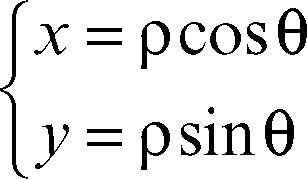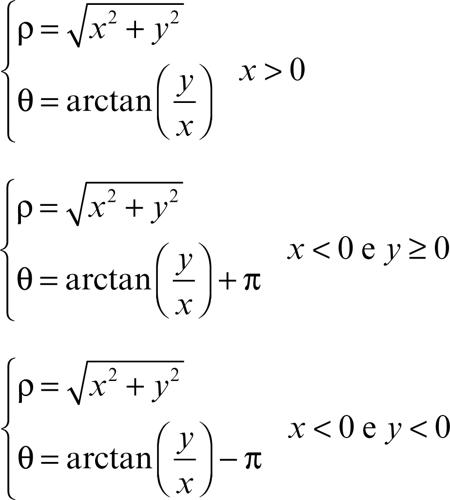riferimento, cambiamento di
riferimento, cambiamento di
riferimento, cambiamento di può intendersi sia come trasformazione che agisce sugli assi del riferimento, lasciando fissi tutti gli altri punti, sia come trasformazione del sistema di coordinate. In generale, un punto P di uno spazio S di dimensione n, dotato di un sistema di riferimento R, è biunivocamente associato a una ennupla ordinata di numeri reali (x1, ..., xn) dette coordinate non omogenee del punto. Introducendo in S un nuovo sistema di riferimento R′, lo stesso punto P è biunivocamente associato a una nuova ennupla ordinata di numeri reali (x1′, ..., xn′). Per stabilire come si modificano le coordinate di un punto generico e come si modificano le equazioni di determinati luoghi nel cambiamento di riferimento risulta utile poter stabilire, dove possibile, relazioni del tipo
e le loro inverse
dette rispettivamente, equazioni di una trasformazione di coordinate ed equazioni della trasformazione inversa. Per semplicità, in questa voce, ci si riferirà nel seguito al piano; tuttavia quanto detto si può estendere allo spazio tridimensionale o più in generale a uno spazio di dimensione n.
Traslazione degli assi
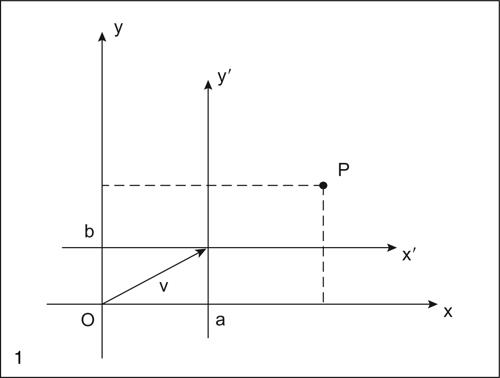
Dagli assi del riferimento Oxy si ottengono, mediante una traslazione di vettore v di componenti (a, b), gli assi del nuovo sistema di riferimento O′x′y′. Tra le coordinate (x, y) e (x′, y′ ) di un medesimo punto P, rispettivamente nel vecchio e nel nuovo riferimento, valgono le relazioni:
e le inverse
Le prime sono utilizzate per ricalcolare le coordinate di un punto nel nuovo sistema di riferimento, le seconde per ridefinire l’equazione di un luogo nel nuovo sistema di riferimento. Per esempio, se si prendono a = 2 e b = −1, le precedenti equazioni di trasformazione di coordinate assumono, rispettivamente la forma:
Se P(5, 7) è un punto riferito a Oxy, applicando le prime equazioni, nel riferimento O′x′y′ risulta P(3, 8). Se invece, per esempio, si ha una parabola avente nel riferimento Oxy equazione y = −x 2 + x − 3, applicando le trasformazioni inverse, la sua equazione nel riferimento O′x′y′ è y′ − 1 = − (x′ + 2)2 + (x′ + 2) − 3, cioè y′ = −(x′ )2 − 3x′ − 4.
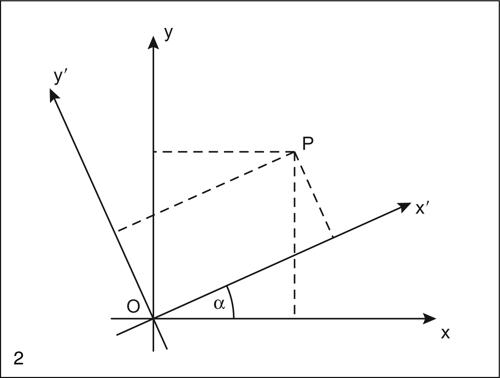
Rotazione degli assi
Gli assi del nuovo sistema di riferimento O′x′y′ si ottengono dagli assi del vecchio sistema Oxy, ruotati di un angolo α intorno all’origine O. Tra le coordinate (x, y) e (x′, y′ ) di un medesimo punto P, rispettivamente nel vecchio e nel nuovo riferimento, valgono le relazioni:
cioè
Rototraslazione degli assi
Il nuovo sistema di riferimento O′x′y′ si ottiene eseguendo sugli assi del vecchio sistema Oxy prima una rotazione di un angolo α intorno all’origine O e, successivamente, una traslazione di vettore v di componenti (a, b). Le equazioni del cambiamento sono:
cioè
Da coordinate cartesiane a coordinate polari e viceversa
Come trasformazione del sistema di coordinate, nel piano, si può considerare il passaggio da coordinate cartesiane ortogonali a coordinate polari e viceversa. Le relazioni che intercorrono tra le coordinate cartesiane (x, y) e le coordinate polari (ρ, θ) di un medesimo punto P del piano sono espresse dalle seguenti equazioni di trasformazione:
Per determinare le equazioni della trasformazione inversa, con polo coincidente con l’origine, asse polare coincidente con il semiasse positivo delle ascisse e stessa unità di misura, occorre distinguere diversi casi per esprimere correttamente l’anomalia θ ∈ (−π, π] e per ogni punto diverso dall’origine si ha:
avendo indicato con arctan la funzione arcotangente.