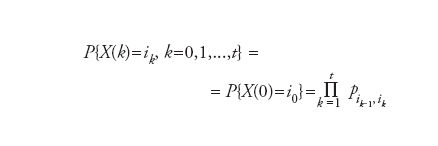catena di Markov
Catena di Markov
Si dice markoviano un processo stocastico la cui evoluzione da un valore fissato a un tempo t non dipenda da quella precedente a t stesso. In altri termini, il passato e il futuro del processo sono tra ;loro indipendenti per ogni presente noto e fissato. Più precisamente, sia X(t) (t∈T, con T sottoinsieme della retta reale) un processo markoviano su uno spazio di probabilità (Ω,F,P), a valori in uno spazio di misura (E,B). Allora la sua distribuzione di probabilità soddisfa, per ogni t1〈t2〈...〈tr〈 tr1〈...〈 tn, la relazione
P{X(tr+1)〈xr+1,...,X(tn)〈 xn |
|X(t1)=x1,..., X (tr)=xr} =
= P{X(tr+1)〈 xr+1,...,X(tn)〈 xr | X(tr)=xn}
dove P{A|B} indica la probabilità dell’evento A condizionata dal realizzarsi dell’evento B.
Un processo di Markov in cui T sia un sottoinsieme (finito o infinito) dei numeri naturali ℕ è detto catena di Markov, anche se talvolta tale denominazione è riservata a processi di Markov a valori in un insieme E al più numerabile.
In quest’ultimo caso, nell’ipotesi che T sia un intervallo della retta reale ℝ, si parla di catena di Markov a tempo continuo.
Nel seguito considereremo solo catene a tempo discreto, che indicheremo con il simbolo X(k) (k=0,1,...).
Nella descrizione probabilistica di una catena di Markov X(k) giocano un ruolo essenziale le probabilità di transizione pιj(k)=P{X(k+1)=j |X(k)=i }, con i,j ∈E.
Nel caso esse siano indipendenti dal tempo la catena è detta omogenea (nel tempo) e pιj(k)=pιj. La matrice ( pιj) (con un numero di righe e colonne pari alla cardinalità dell’insieme E degli stati) è detta matrice di transizione. La probabilità di una data evoluzione (o traiettoria) X(k)=iκ (k=0,1,...,t) è espressa in termini delle probabilità di transizione e della distribuzione iniziale P{X(0)=i } come segue:
Due stati i e j si dicono comunicanti se esistono k1 e k2 tali che pιj. (k1)>0 e pjι (k2)>0.
Uno stato i è detto inessenziale se esiste uno stato j tale che pij (k1)>0 per qualche k1>0 e pjι (k)=0 per ogni k∈ℕ.
Lo spazio degli stati E di una catena si decompone quindi in stati inessenziali e essenziali. Questi ultimi si dividono a loro volta in classi disgiunte di stati comunicanti.
Una catena di Markov è detta irriducibile (o non decomponibile) se tutti gli stati appartengono a una e una sola classe di stati comunicanti.
→ Simulazioni di processi fisici mediante calcolatore