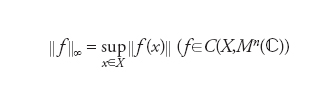fibrato vettoriale
fibrato vettoriale
Un fibrato {B,X,F,τ} con spazio totale B, spazio di base X e proiezione canonica τ:B→X è detto fibrato vettoriale se: (a) la fibra tipica X è uno spazio vettoriale di dimensione finita e la sua topologia relativa (come sottoinsieme di B) coincide con la sua topologia come spazio vettoriale; (b) ogni banalizzazione locale φα:τ−1(x)⊂B→Uα×F⊂X×F (dove x∈X) è un’applicazione lineare. Un fibrato complesso, per es., è un fibrato vettoriale con fibra tipica ℂ{[ (n∈ℕ). Il più semplice esempio di fibrato complesso con base X è il prodotto cartesiano B=X×ℂ{[ (detto fibrato banale) e a partire da esso è possibile costruire fibrati vettoriali non banali come segue. Consideriamo C*-algebra C(X,M{[(ℂ)) delle funzioni continue dallo spazio X (supposto compatto, di Hausdorff e connesso) a valori nello spazio M{[(ℂ) delle matrici n×n a valori complessi con
dove la norma a secondo membro è una qualunque norma su M{[(ℂ)). Una funzione p∈C(X,M{[(ℂ)) è un idempotente o proiettore (ovvero p2=p) se e solo se ogni p(x) lo è in M{[(ℂ). Un tale idempotente definisce un fibrato vettoriale {B,X,F,τ} su X con fibra su x uguale a τ−1(x)=p(x)ℂ{[. Più interessante è la validità della proposizione inversa: dato un fibrato vettoriale complesso {B,X,F,τ} su uno spazio compatto di Hausdorff connesso X e fibra tipica ℂ{[, esistono un intero m>n e un idempotente p∈C(X,M{[(ℂ)) tali che B⊂X×ℂ{[, con τ−1(x)=p(x)ℂ{[. L’idea della dimostrazione è costruire un nuovo fibrato vettoriale {B′,X,F′τ′} su X tale che B⊕B′ (la somma diretta è definita come somma diretta delle fibre per ciascun x∈X) sia triviale, ovvero equivalente a X×ℂ{[. Anche nel caso di fibrati vettoriali si definisce lo spazio ΓΓdelle sezioni continue: esso è costituito di funzioni continue su X a valori nello spazio vettoriale F ed è dunque a sua volta uno spazio vettoriale con le usuali operazioni di somma tra funzioni e moltiplicazione per scalari. Su di esso, si ottiene un’azione π∮ su Γ dell’algebra C(X) delle funzioni continue da X in ℂ definita da π∮(f)Ψ(x)=f(x)Ψ(x) con f∈C(X), Ψ(x)∈Γ. Lo spazio Γ può allora essere considerato un modulo su C(X). Per questa via è possibile ottenere il celebre teorema di Serre-Swan, che determina una corrispondenza biunivoca tra fibrati vettoriali complessi (su spazi compatti di Hausdorff connessi) e particolari moduli sull’algebra C(X).