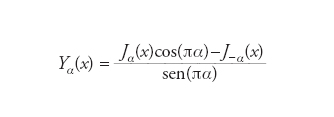funzioni di Bessel
funzioni di Bessel
Stabilite per la prima volta nel Settecento da Daniel Bernoulli e generalizzate nel corso dell’Ottocento da Friedrich Bessel, ricoprono un ruolo importante in diversi campi applicativi, quali la propagazione delle onde, i potenziali statici, i problemi di diffusione, la propagazione del calore in forme cilindriche, l’analisi modale delle vibrazione di membrane sottili vincolate sul bordo (la forma di base degli strumenti musicali denominati membranofoni). Compaiono inoltre nell’espressione formale della modulazione di frequenza con segnali sinusoidali, ricoprendo così un ruolo essenziale anche in elaborazione del segnale. Le funzioni di Bessel di prima specie Jα(x), di seconda specie
così come quelle a loro collegate di Hankel (Hα(1,2)(x)=Jα(x)±iY∮(x)), tutte funzioni oscillanti che tendono asintoticamente a zero, sono soluzioni delle equazioni di Bessel, che a loro volta intervengono nelle soluzioni delle equazioni di Laplace e di Helmholtz. Le funzioni di Bessel, che godono di numerose notevoli proprietà e relazioni interne, sono dotate di espressioni asintotiche nell’intorno di zero e infinito mediante funzioni note. Sono inoltre asintoticamente periodiche. Il calcolo numerico delle funzioni di Bessel si effettua grazie alle loro relazioni notevoli e al loro sviluppo in serie di Taylor.
→ Musica elettronica ed elettronica musicale