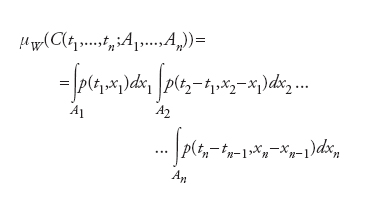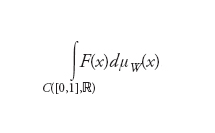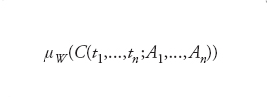misura di Wiener
misura di Wiener
Una misura di probabilità sullo spazio C([0,1],ℝ) delle funzioni continue a valori reali sull’intervallo chiuso [0,1] definita come segue. Siano 0⟨t1⟨...⟨tν≤1 punti arbitrari di [0,1] e A1,...,Aν sottoinsiemi boreliani della retta reale ℝ (unioni arbitrarie o intersezioni finite di intervalli chiusi). Indichiamo infine con C(t1,...,tν;A1,...,Aν) l’insieme di tutte le funzioni x∈C([0,1],ℝ) tali che x(tκ)∈Aκ, k=1,...,n. Se gli Aκ sono intervalli chiusi in ℝ allora gli insiemi C(t1,...,tν;A1,...,Aν) sono detti cilindrici: gli stessi Aκ sono le basi di questi ‘cilindri’. La misura di Wiener μϬ è definita dalla formula
dove p(t,x)=1/√__2πt e−χ2/2τ. La misura può essere poi estesa alla σ-algebra dei sottoinsiemi boreliani di C([0,1],ℝ) generata dai C(t1,...,tν;A1,...,Aν). Sia ora F:C([0,1],ℝ)→ℝ un funzionale lineare a valori reali misurabile (nel senso di Lebesgue) rispetto alla misura μϬ. In maniera analoga alla procedura utilizzata per definire dalla misura di Lebesgue il corrispondente integrale, si definisce allora l’integrale di Wiener
Misura e integrale di Wiener hanno costituito il primo esempio di estensione della teoria dell’integrazione a spazi di dimensione infinita e furono introdotti da Norbert Wiener nel 1923 nel quadro dei suoi studi sul moto browniano. La funzione p(t,x) assume qui il ruolo di densità di probabilità per la posizione x di una particella a un fissato tempo t e la quantità
appare come la probabilità che, nel suo moto, agli istanti t1,...,tν la particella stessa si trovi all’interno degli insiemi A1,...,Aν.