multivettore
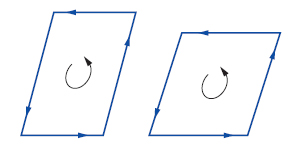
In matematica, una delle possibili generalizzazioni della nozione di vettore. Si consideri uno spazio euclideo a n dimensioni, e in esso un sistema ordinato di r vettori uscenti da uno stesso punto. Si tratta ora di raggruppare in opportune classi di equivalenza tutti i possibili sistemi di tale tipo: ogni classe costituirà un m. di dimensione r o r-vettore. Il procedimento è analogo a quello che nel caso r = 1 permette di passare dalla nozione di segmento orientato a quella di vettore come sinonimo di classe di segmenti orientati tra loro equipollenti, cioè aventi la stessa direzione, lo stesso verso e la stessa lunghezza. Precisamente, due r-ple ordinate di vettori si pongono in una stessa classe quando appartengono a un medesimo spazio euclideo di dimensione r, danno a tale spazio la medesima orientazione e infine individuano due parallelotopi o r-parallelepipedi (ossia parallelepipedi r-dimensionali) di uguale volume. Se, poi, un r-vettore appartiene a uno spazio euclideo di dimensione inferiore a r si dirà che esso rappresenta il m. nullo. Nei casi in cui è r=2, r=3, i m. prendono il nome di bivettori e trivettori, rispettivamente; in figura sono indicati due parallelogrammi orientati che individuano uno stesso bivettore: infatti i due parallelogrammi racchiudono due superfici della stessa estensione e il cui contorno è ugualmente orientato. La nozione di m. è di notevole importanza nella teoria delle forme esterne, in quanto ogni forma esterna di grado r dà luogo a un’applicazione lineare degli r-vettori sul campo dei reali.