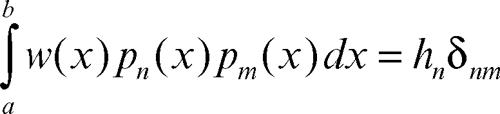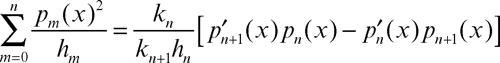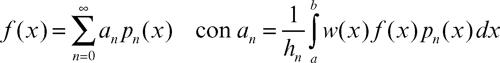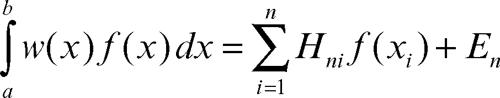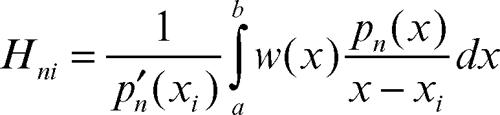polinomi ortogonali
polinomi ortogonali
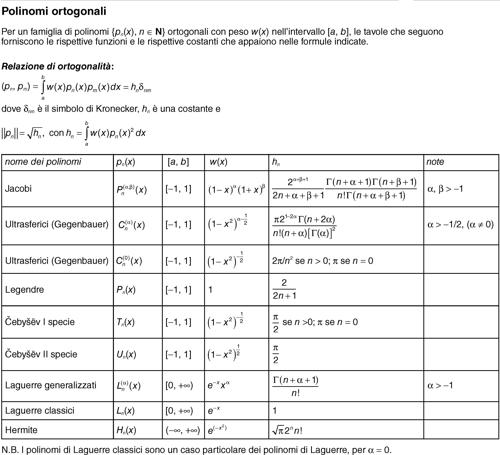
polinomi ortogonali denominazione di diverse famiglie di polinomi unite da numerose caratteristiche comuni, che ne consentono una descrizione unificata. Se una famiglia {pn(x), n ∈ N} è formata da polinomi di grado n che soddisfano la condizione
dove δnm è il simbolo di → Kronecker e hn una costante, si dice che tali polinomi sono ortogonali rispetto al peso w(x) nell’intervallo [a, b]; tale intervallo può essere anche illimitato. Il peso w(x), almeno nei casi cosiddetti classici, è una funzione continua misurabile e maggiore o uguale a 0 in [a, b], purché l’integrale su [a, b] sia positivo. La costante di normalizzazione hn può essere sempre posta uguale a 1 (si parla allora di polinomi ortonormali), ma tale scelta non è usuale nei polinomi classici.
Tra le proprietà di una famiglia di polinomi ortogonali si ricordano le seguenti:
• gli zeri di pn(x) sono tutti semplici e cadono all’interno di [a, b];
• tra due zeri successivi di pn(x) cade uno (e uno solo) zero di pn+1(x);
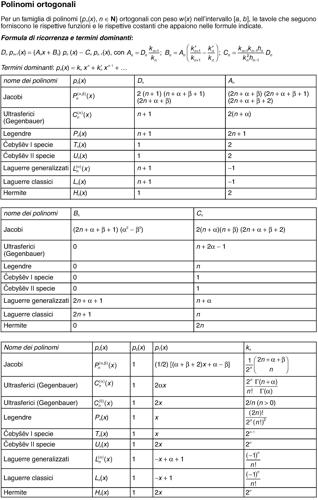
• tre polinomi consecutivi sono legati da una relazione di ricorrenza della forma
• vale la cosiddetta formula di Christoffel-Darboux, dal nome del matematico tedesco E.B. Christoffel e del francese J.G. Darboux:
dove kn è il coefficiente di xn in pn(x). Per y → x se ne ottiene la formula
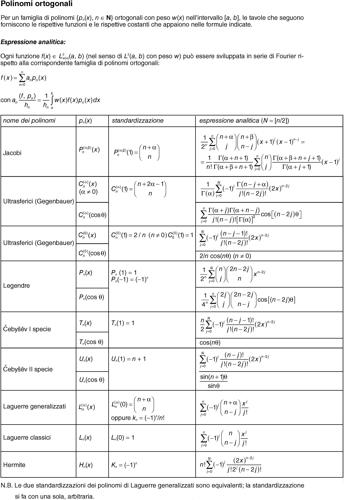
• ogni funzione ƒ(x) ∈ L2w(x)(a, b) può essere sviluppata in serie di Fourier rispetto alla corrispondente famiglia di polinomi ortogonali. È cioè:
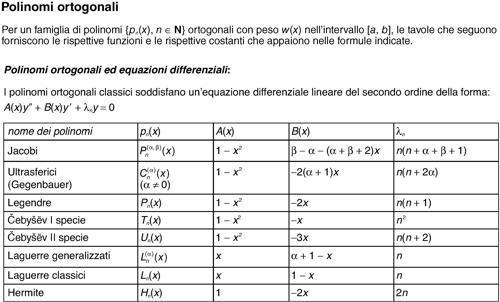
• i polinomi ortogonali classici soddisfano un’equazione differenziale lineare del secondo ordine della forma A(x)y″ + B(x)y′ + λny = 0;
• vale per essi la cosiddetta formula di Rodrigues, dal nome del banchiere e matematico francese, nonché riformatore sociale, B.O. Rodrigues che la elaborò nel 1816:
nella quale X(x) è un polinomio al più di secondo grado è Kn è una costante;
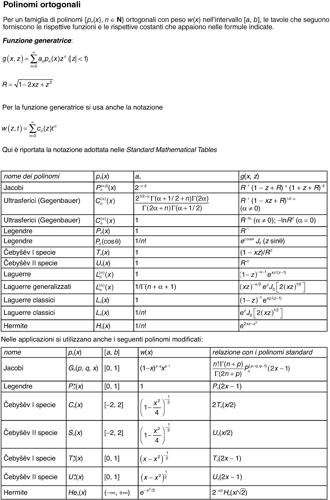
• una funzione generatrice per una famiglia di polinomi è una funzione F(z) che ammette lo sviluppo di Maclaurin
Le prime e principali applicazioni dei polinomi ortogonali sono nel campo delle equazioni differenziali alle derivate parziali, quando per separazione delle variabili si ottengono le equazioni lineari che li descrivono e quindi i corrispondenti sviluppi di Fourier.
Altre importanti applicazioni si hanno nella integrazione numerica, sussistendo le formule di quadratura gaussiana
dove xi sono gli zeri del polinomio pn(x) e
sono opportune costanti. L’errore En ha la forma
essendo ξ un opportuno valore appartenente all’intervallo (a, b).
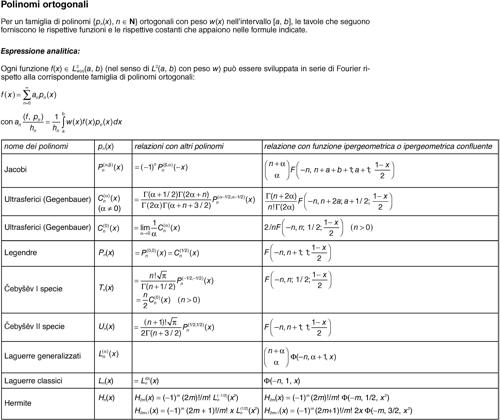
Le più importanti famiglie di polinomi ortogonali sono casi particolari della funzione ipergeometrica o della funzione ipergeometrica confluente, e sono:
• i polinomi di → Jacobi Pn(α, β)(x), con α, β > −1, corrispondenti al peso w(x) = (1 − x)α(1 + x)β nell’intervallo [−1, 1];
• i polinomi di → Laguerre generalizzati Ln(α)(x), con α > −1, ortogonali in [0, +∞) rispetto al peso e−xxα;
• i polinomi di → Hermite Hn(x), ortogonali in (−∞, +∞) rispetto al peso
Tra questi polinomi, specificando i parametri, si ottengono famiglie particolarmente importanti:
• i polinomi ultrasferici o di Gegenbauer:
dove Γ è la funzione di → Eulero;
• i polinomi sferici o di → Legendre:
• i polinomi di → Čebyšëv di prima specie
e di seconda specie
• i polinomi di → Laguerre:
Tra le loro applicazioni sono degne di nota:
• lo studio dell’equazione di → Laplace in coordinate sferiche, per i polinomi di Legendre;
• lo studio dell’equazione di → Schrödinger per l’atomo idrogenoide, per i polinomi di Laguerre generalizzati;
• l’interpolazione di minimo errore, per i polinomi di Čebyšëv di prima specie. Essa si basa sulla proprietà Tn(cosθ) = cos(nθ), per cui |Tn(x)| ≤ 1, ottimale per i polinomi aventi lo stesso grado e lo stesso coefficiente direttore;
• le formule di quadratura gaussiana, dette appunto di Gauss-Legendre, Gauss-Laguerre, Gauss-Hermite, per tali polinomi.
Numerosissime sono le formule che coinvolgono queste famiglie; per quelle di ricorrenza, le funzioni generatrici e le formule di Rodrigues si rimanda alle Tavole dei polinomi ortogonali.