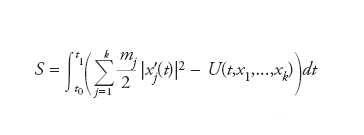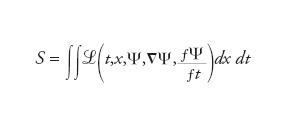principio variazionale
principio variazionale
Corrispondenza tra le soluzioni di un’assegnata equazione differenziale e i punti critici di un opportuno funzionale. I modelli della fisica matematica sono essenzialmente scritti mediante equazioni differenziali a cui si aggiungono le condizioni al contorno e/o iniziali; in molti casi, le soluzioni possono essere riguardate come punti stazionari di un opportuno funzionale associato al sistema, detto funzionale d’azione (o funzionale energia). Per es., le equazioni del moto di un sistema di k particelle di massa mj e con posizione assegnata al tempo t da xj(t)∈ℝ3, j=1,...,k, sono ottenute come equazioni di Euler-Lagrange relative al funzionale
dove U rappresenta l’energia potenziale del sistema. Per intervalli di tempo (t0,t1) sufficientemente piccoli, si può dimostrare che tra tutte le possibili traiettorie, il sistema xj si evolve lungo la traiettoria che minimizza l’azione S (principio di minima azione). Analogamente, la dinamica di un campo, Ψ(x,t):ℝ3+1→ℝk, è ottenuta considerando punti stazionari dell’azione
dove ℒ è la densità lagrangiana del sistema.
→ Fisica matematica; Variazioni, calcolo delle