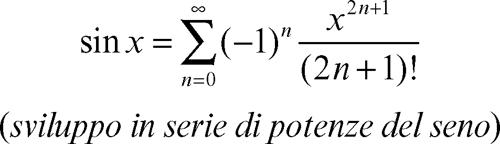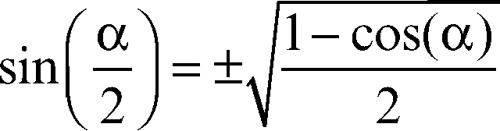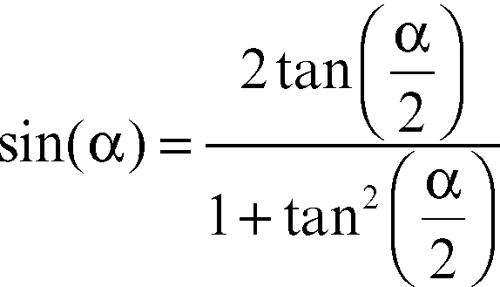seno

seno

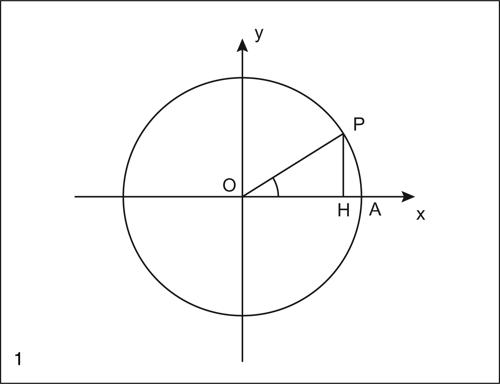
seno di un angolo acuto α di un triangolo rettangolo, è il rapporto tra il cateto opposto all’angolo α e l’ipotenusa. Per la proprietà di → similitudine dei triangoli, tale rapporto è indipendente dal triangolo considerato e dipende solo dall’ampiezza dell’angolo. È indicato con il simbolo sin(α) o sinα e, in Italia, anche con senα. Per generalizzare la definizione ad angoli di ampiezza qualunque si considera una circonferenza centrata nell’origine di un riferimento cartesiano e di raggio unitario (detta circonferenza goniometrica). Data un’ampiezza α, si considera quindi quell’angolo di tale ampiezza α che ha per lati il semiasse positivo delle ascisse e una semiretta uscente dall’origine degli assi, in senso antiorario se α è positivo, orario altrimenti. Il seno di α è allora l’ordinata del punto P in cui tale semiretta interseca la circonferenza goniometrica; il coseno di α è invece la sua ascissa. Come conseguenza immediata del teorema di → Pitagora, vale, qualunque sia il numero reale α, l’identità fondamentale della trigonometria: cos²α + sin²α = 1.

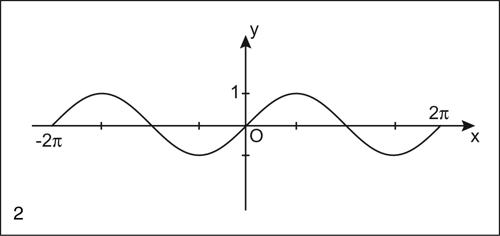
Con tale generalizzazione ad angoli orientati di ampiezza un qualunque numero reale, anche negativo, si definisce la funzione goniometrica di variabile reale y = sin(x), il cui grafico è una curva detta sinusoide, che è definita in tutto R, ha come immagine [−1, 1] (perché −1 ≤ sin(x) ≤ 1 per ogni x) ed è periodica di periodo 2π. La funzione seno è dispari, continua e differenziabile e la sua derivata è:

Più precisamente, la funzione seno è differenziabile infinite volte ed è analitica, vale a dire coincide con il suo sviluppo in serie di potenze (→ funzione analitica). Vale pertanto la seguente formula:

Per il seno valgono le seguenti formule:

a) sin(α + β) = sin(α)cos(β) + cos(α)sin(β)

(formula di addizione)

b) sin(α − β) = sin(α)cos(β) − cos(α)sin(β)

(formula di sottrazione)

c) sin(2α) = 2 sin(α)cos(α)

(formula di duplicazione)

d)

(formula di bisezione)

Nella formula di bisezione il segno positivo o negativo va dedotto considerando il quadrante in cui cade l’angolo di ampiezza α/2.

e)

(formula del quadrato del seno)

f)

(formula parametrica)