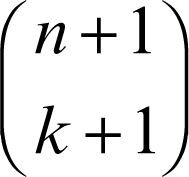simplesso euclideo

simplesso euclideo

simplesso euclideo in topologia combinatoria, unità elementare risultante dalle triangolazioni (ossia dalle scomposizioni) di uno spazio topologico. Un simplesso euclideo di dimensione n è il tipo più semplice di poliedro di dimensione n (→ politopo). I simplessi euclidei di dimensione −1, 0, 1, 2 e 3 sono, rispettivamente, l’insieme vuoto, un punto, un segmento, un triangolo e un tetraedro. Formalmente, un simplesso euclideo di dimensione n è un sottoinsieme di uno spazio R^m (con n ≤ m) dato dall’inviluppo convesso di n + 1 punti x₀, x₁, ..., x_n in posizione generica (ossia tali che i vettori x₁ − x₀, x₂ − x₁, ..., x_n − x_n−1 siano linearmente indipendenti). I punti che generano il simplesso euclideo sono chiamati vertici. Nonostante la possibile confusione con il simplesso astratto (→ complesso simpliciale astratto), è comune l’uso del termine simplesso in luogo di simplesso euclideo. Un simplesso euclideo di dimensione n è anche detto n-simplesso. Una faccia di dimensione k (−1 ≤ k ≤ n) di un simplesso σ di dimensione n è un simplesso di dimensione k individuato da k + 1 vertici distinti di σ. Una faccia di σ è dunque un sottoinsieme di σ. Ogni simplesso σ di dimensione n ha esattamente

facce di dimensione k (→ coefficiente binomiale). Per esempio, un simplesso di dimensione 3 (un tetraedro) ha 1 faccia tridimensionale, 4 facce bidimensionali (le facce in senso ordinario), 6 facce unidimensionali (gli spigoli), 4 facce di dimensione 0 (i vertici) e 1 faccia di dimensione −1.

Il simplesso euclideo standard di dimensione m − 1 è l’inviluppo convesso dei punti e₁, e₂, ..., e_m dati dalla base canonica di R^m. Assegnare un’orientazione a un n-simplesso euclideo σ consiste nel fissare uno dei possibili ordinamenti totali dei suoi vertici, considerando equivalenti due ordinamenti se si possono ottenere uno dall’altro attraverso un numero pari di scambi (cioè attraverso una permutazione pari). Per ogni simplesso σ si hanno così due possibili orientazioni. Una volta assegnata un’orientazione, σ prende il nome di simplesso euclideo orientato. Per esempio, il simplesso di dimensione 2 di vertici a, b e c ha le seguenti due orientazioni: